Qu'est ce qu'un différentiel ? Quel est son rôle ?
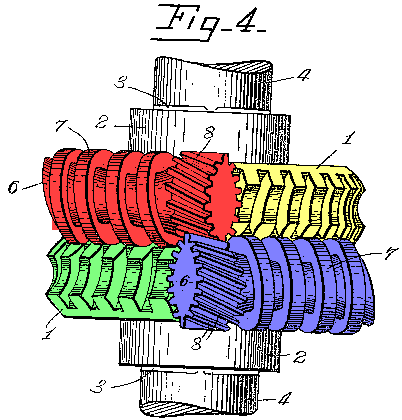
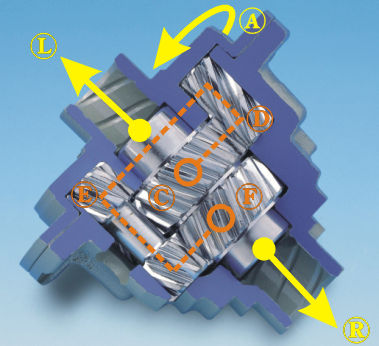
Le différentiel est un système d'engrenage issu le l'horlogerie. Son rôle est de distribuer suivant une répartition fixe au frottement près (et oui !) tout en permettant une différence de vitesses entre ses sorties. Il existe différents types de différentiel du point de vue structure mais dans l'automobile, le principal type utilisé est le différentiel à pignons coniques, vient ensuite le différentiel à double train épicycloïdale assez souvent utilisé comme différentiel central (mais c'est quoi un différentiel central ?).
Maintenant, pour un tel dispositif est-il nécessaire ?
En virage, les 2 roues d'un même essieu ne décrivent pas un cercle de même diamètre, elles ne tournent donc pas à la même vitesse...il faut donc une certaine liberté entre celles-ci... et il est de même pour les essieux, d'où la présence d'un différentiel dit central (ou interpont) entre les essieux pour les transmissions 4x4 dites permanentes mais nous y reviendrons...
Maintenant, parlons répartition du couple. On aborde une notion pas toujours évidente. La base est simple, un roue ne peut pas transmettre plus de couple au sol qu'elle n'a d'adhérence. Ainsi le couple qu'une roue reçoit du différentiel est toujours inférieur à l'adhérence de celle-ci. Si on tente d'en passer plus, cela patine, l'adhérence chute, le couple transmissible (celui que la roue peut passer au sol) diminue et donc le couple que reçoit la roue diminue et le couple nécessaire à l'avancement diminue... Ainsi, plus cela patine, plus l'adhérence est proche de 0 et plus le couple que la roue reçoit est aussi proche de 0.
Maintenant, revenons à l'échelle du différentiel. Comme dit plus haut, un différentiel distribue le couple suivant une répartition fixe, ce qui veut dire que si le couple envoyé à une roue diminue, la roue opposée reçoit elle aussi moins de couple. Dans le cas extrème où une roue aurait une adhérence nulle et donc ne recevait pas de couple, l'autre roue n'en recevait pas non plus... d'où l'immobilisation si une roue est sur une plaque de glace et l'autre sur le goudron pour une auto 2 roues motrices.
Mathématiquement, le couple total que reçoit le différentiel est égale à 2 fois le couple transmissible avec l'adhérence la plus faible...
Posons C1, le couple que peut recevoir la roue 1, C2 le couple que peut recevoir la roue 2 et CT, le couple total que peut transmettre le différentiel.
On a alors:
C1=kC2 ou k est le facteur de répartition. k égale 1 pour un différntiel symétrique.
et CT=C1+C2...
Avec cela on comprend donc que CT dépend du couple qu'un roue peut transmettre ce que peut transcrire de la manière suivante:
En posant l'hypothèse que le différentiel est symétrique, c'est à dire que sa répartition est égale pour les 2 roues.
On obtient C1=C2=mini[C1,C2] et donc que CT=2 x mini[C1,C2]
Je sais, c'est des maths et c'est chiant
Compliquons les choses et introduisons les frottements internes.
Quand les 2 roues tournent strictement à la même vitesse, tout le système d'engrenage interne est inactif, les frottements sont donc nuls mais ce n'est pas la cas en virage.
Posons l'hypothèse que la roue 1 est à l'interieur du virage, c'est donc elle qui tourne le plus lentement. A l'inverse, la roue 2 étant à l'exterieur, c'est donc elle qui tourne le plus rapidement.
Et les frottements dans tout cela ? Bien, ces frottements vont tendre à égaliser les vitesses des roues en s'opposant à l'effet du différentiel. Cela qui veut qu'ils vont essayer d'accélérer la roue la plus lente et ralentir la roue la plus rapide, ok ?
On a donc, au niveau des couples que reçoivent les roues, il y a des frottements qui vont s'additionner au niveau la roue la plus lente (sous force d'un apport de couple suplémentaire et l'autre des frottements qui vont se soustraire au niveau de la roue la plus rapide (sous forme de couple de sens inverse).
On a donc pour un différentiel symétrique:
C1=CT/2 + CF où CF est la moitié des frottements
C2=CT/2 - CF
Si on fait C1 - C2, il apparait une autre chose importante, la dissymétrie de couple:
C1 - C2 = 2CF
Mais cela veut dire quoi cette dissymétrie ?
Pour l'expliquer, j'ajoute ici une autre équation de base du différentiel:
W1 + W2 = 2Wb où W1 est la vitesse angulaire (la vitesse de rotation) de la roue 1 et W2 la vitesse angulaire de la roue 2. Enfin Wb est la vitesse angulaire du boitier de différentiel.
Les conséquénces ? Dans notre cas (la roue 2 tourne la plus vite), plus W2 se rapproche de 2Wb, plus W1 tend vers 0, toujours ok ?
Pour notre histoire de dissymétrie.
Si la roue 2 accélère et tend vers 2Wb car elle perd de l'adhérence, alors la roue 1 tend vers 0 ce qui veut dire qu'au niveau du couple la roue perdant de l'adhérence tend vers 0. ok ?
Introduisons cela dans la formule de la dissymétrie:
C1 + O = 2CF et donc C1 = 2 CF
Cela veut dire que la roue la plus lente reçoit un couple équivalent à aux frottement interne (CF c'est la moitié des frottements).
Mais alors pourquoi si une roue est sur de la glace et l'autre sur du bitume, l'auto reste immobilisée alors que cette dernière reçoit les frottements internes ? Simplement parce que ces frottements sont trop faibles (tellement qu'on peut facilement les négligeabler), bien inférieurs au couple nécessaire pour faire avancer l'auto...
Et c'est sur ce point -les frottements internes- que les différentiels à glissement limité vont agir...
Comme vous l'avez un peu vu les lois de base théoriques du différentiel ne sont plus tout à fait respectées avec les frottements internes... et cela ne s'améliore pas avec les glissements limités...
A noter que parfois le terme d'autobloquant est utilisé mais, il me parait un peu impropre car différentiel à glissement limité ne se bloque que partiellement, d'où le terme "limité"
Parlons du terme souvent entendu de "tarage". Pour un différentiel à glissement limité, ce terme représente le pourcentage de blocage du différentiel. Donc plus ce pourcentage est élevé, plus le blocage est complet. Ce tarage se calcule de la manière suivante:
T(%) = 100 x (C1 - C2)/CT
où C1 et C2 sont les couples respectivement de la roue lente et de la roue rapide comme définis dans le message précédent.
Ainsi, on voit que plus le tarage est important, plus la dissymétrie est important. Plus précisément, plus la tarage tend vers 100%, plus la dissymétrie tend vers CT.
Dans les véhicules du grand public, le tarage varie pour la majorité des cas entre 20 et 40% (c'est à dire que la roue lente reçoit 20 à 40 % du couple) alors que des autos de compétition vont bien au delà, dépassant parfois les 80%. Mais de telles valeurs limitent fortement voir annulent l'effet du différentiel, en particulier pour un couple total (CT) faible à basse vitesse, ce qui pose des problèmes de sollicitation des transmissions et des problèmes de facilité de comportement routier.
La solution est de concevoir un différentiel à glissement limité donc les frottements internes sont faibles quand le couple total est faible et qui croît ensuite. On peut alors jouer sur les frottements internes initiaux.
On peut représenter cela sur un graphique avec une droite d'équation suivante:
C1 (roue lente) = a x C2(roue rapide) + 2CFi où a (>1) correspond au coéfficient directeur de la droite, c'est à dire l'accroissement de frottements internes et CFi les frottements initiaux.
On retrouve la formule de base de la dissymétrie quand C2 est égale 0 avec C1 = 2CFi mais quand le couple C2 augmente (et donc CT), C1 augmente aussi mais de manière beaucoup plus rapide... (faudrait que je fasse cette courbe, c'est plus explicite)
Maintenant reprenons la formule du tarage avec nos nouvelles données.
On a:
C1 = a x C2 + 2CFi
CT = C1 + C2 donc CT = a x C2 + 2CFi + C2 = C2 x (a+1) + 2CFi
Ainsi on a = C1 - C2 = a x C2 + 2CFi - C2 = C2 x (a-1) + 2 CFi
Si on introduit cela dans la formule du tarage, on a:
T(%)= 100 x [C2 x (a-1) + 2 CFi]/[C2 x (a+1) + 2CFi]
CFi est très faible devant les autres couples, on peut donc le négliger.
on obtient donc:
T(%)= 100 x [C2 x (a-1)]/[C2 x (a+1)] = 100 x (a-1)/(a+1) ce qui est une constante caractéristique du glissement limité.
Ainsi la différence de couple entre la roue lente et la roue rapide est totalement indépendante de la différence de vitesses entre celle-ci, d'où des problèmes de d'auto-bloquage dès qu'il y a une différence de vitesses entre les roues se faisant sentir sur le comportement routier.
Je sais, que de maths...